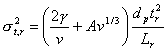Průtokový kapilární reaktor

Trubkový náplňový reaktor

Literatura

Derivatizace za kolonou (post-column derivatization) se někdy rovněž nazývá on-line derivatizace a jedná se o průtočný reaktor, který je umístěn za chromatografickou kolonu. V průběhu reakce dochází k rozmývání zóny v celém systému, které je nutno potlačit na minimum, čehož se dosáhne vhodnou konstrukcí reaktoru, směšovačů a spojovacího potrubí.

Tok kapaliny reaktorem by se měl svými vlastnostmi blížit pístovému toku bez axiálního promíchávání mobilní fáze. Podle účelu lze pak používat různé typy reaktorů a to buď prázdné, které jsou vhodné pro rychlé reakce, kdy doba zdržení t_r v reaktoru je menší než 30 sekund, nebo náplňové, které jsou vhodné pro chemické reakce pomalé, kdy vyžadujeme 30 s > t_r < 5 minut.

Rozšiřování elučních zón, které přicházejí do reaktoru z kolony a procházejí jím za současné tvorby derivátu, je uvnitř reaktoru způsobováno axiální disperzí,^[1] která se vyjadřuje rozptylem s_t,r², resp. standardní odchylkou s_t,r, kde r značí příspěvek reaktoru (vlastního kromě kolonového příspěvku s_t,c:

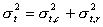
Průtokový kapilární reaktor

Pro standardní odchylku průtokového kapilárního reaktoru platí:

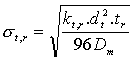
kde parametr k_t,r (<1) vyjadřuje vliv svinutí kapiláry a platí pro dlouhé úzké kapiláry a D_m - koeficient molekulární difúze v reakční kapalině.

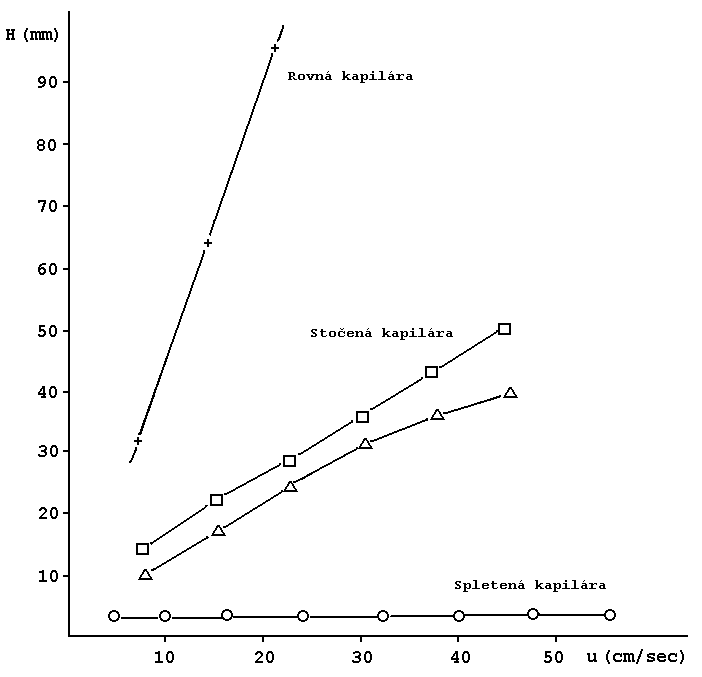
Svinutím rovné kapiláry do šroubovice dojde k potlačení axiální disperze vlivem sekundárního toku, který způsobuje radiální promíchávání. Následkem toho dojde pak zcela k potlačení laminárního proudění. Snížení rozptylu eluční zóny vlivem různého svinutí kapiláry je ukázán na obrázku č. 1. Nejlepších výsledků (vyjádřená jako výška teoreického patra H [mm]) se dosahuje ve spletených kapilárách (tzv. copánek), pokud je kapilára pouze stočená nebo rovná. Detail spletené kapiláry je ukázán na obrázku č. 2.

Obr. č. 1 Rozšíření eluční zóny pro různě svinuté kapiláry - vliv parametru k_t,r

Obr. č. 2 Reakční kapilára - copánek

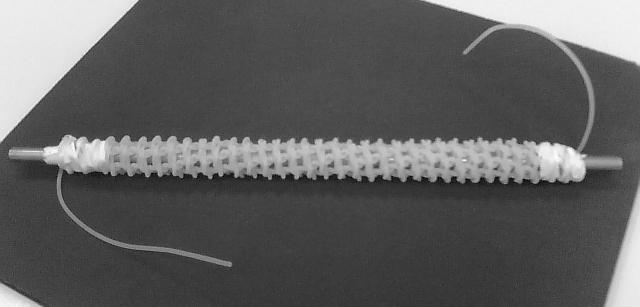
Tlakový spád Dp dosahovaný na úzké kapiláře je dán modifikovanou Poiseuilleovou rovnicí:^[2]

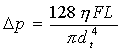
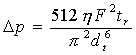
kde d_t je vnitřní průměr kapiláry, t_r- průměrná doba zdržení látky v reaktoru (residence time), L je délka kapiláry, h - dynamická viskozita kapaliny (mPa.s), F -objemový průtok.

Úpravou výše uvedených rovnic dostaneme:

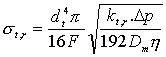
Z rovnice je patrné, že rozmývání zón (rozšiřování píků) je závislé zejména na průměru reakční kapiláry d_t a objemovém průtoku F. Při konstantní hodnotě reakčního času se zmenšujícím se průtokem se rozmývání zón v kapilárním stočeném reaktoru zvyšuje.

Axiální disperzi je možné snížit geometrickým uspořádáním trubkového reaktoru např. jeho spletením, čímž dojde k rozrušení parabolického profilu toku (vlivem geometrické deformace proudnice). Změna geometrického uspořádání se realizuje u kapilárních reaktorů zhotovených z PTFE.^[3],[4]

Trubkový náplňový reaktor

Trubkový náplňový reaktor je trubice, stočená do spirály a naplněná neporézním materiálem. Je-li náplň trubkového reaktoru tvořena skleněnými kuličkami o velmi malém průměru (d_p »10 µm), pak axiální disperze je srovnatelná s disperzí v apilárním reaktoru. Pro rozptyl chromatografické zóny v náplňovém reaktoru platí:

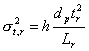
kde h je redukovaná výška teoretického patra, která se vypočte z empirické rovnice vyjadřující vztah mezi redukovanou výškou teoretického patra a redukovanou rychlostí mobilní fáze v = ud_p/D_m v závislosti na vlastnostech a geometrii lože (koeficient g vyjadřující vlastnosti lože a empirická konstanta A daná geometrií lože):^[5]

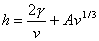
a pak dosazením do předchozí rovnice platí:

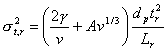
kde L_r je délka náplně reaktoru a t_r je doba zdržení. Z rovnice je patrné, že nejmenších hodnot s_t,r se dosáhne použitím dlouhého reaktoru plněného malými částicemi. Z experimentálních hodnot h jako funkce v v závislosti na geometrii reaktoru a velikosti částeček náplně, je patrné minimum, které udává optimální řešení.^[6]

Literatura

[1]. Horváth C.G., Preiss B.A., Lipsky S.R.: Anal.Chem. 39,1422 (1967).

[2]. Tijssen R.: Anal.Chim. Acta 114, 71 (1980).

[3]. Hofmann K., Halász I.: J. Chromatogr. 199, 3 (1980).

[4]. Engelhardt H., Neue U.D.: Chromatographia 15, 403 (1982).

[5]. Done J.N., Knox J.H.: J. Chromatogr. Sci 10, 606 (1972).

[6]. Deelder R.S., Knipers A.TJ., van den Berg J.H.M.: J. Chromatogr. 255, 545 (1983).

[7]. Extra-Column Band Spreading Concerns in Post-Column Photolysis

[Top of Page]

Last modified:
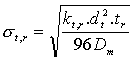
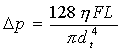
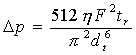
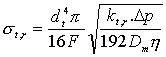
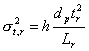