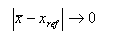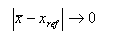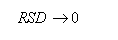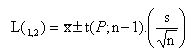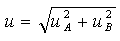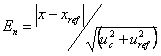Definice

Nejistota měření

Návaznost měření

Definice

Zde si budeme definovat, co je správná a přesná metoda, odchylka a chaba. Dále uvedeme, jaký je rozdíl mezi intervalem spolehlivosti a nejistotou měření.

Správnost, přesnost, chyba a odchylka metody

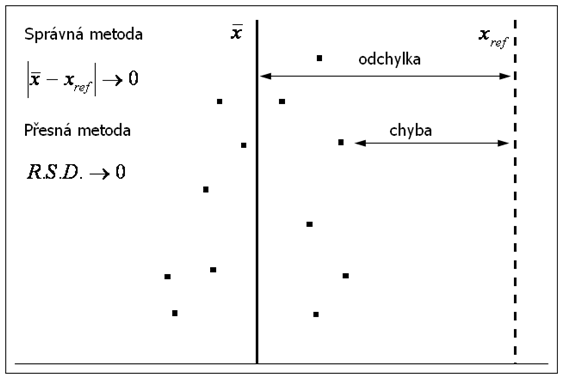
Správnost metody (Accuracy) je definována jako stupeň, do jakého stanovená hodnota analytu ve vzorku odpovídá přijaté referenční hodnotě. Pak platí:

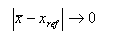
Přesnost metody (Precision) vyjadřuje těsnost souhlasu mezi nezávislými výsledky zkoušek získanými za předem definovaných podmínek. Přesnost se vyjadřuje jako směrodatná odchylka resp. relativní směrodatná odchylka (RSD). Pak platí:

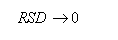
Chyba výsledku (Errors of result) Výsledek zkoušky minus dohodnutá referenční hodnota (x_ref).

Odchylka (Bias) Rozdíl mezi střední hodnotou výsledku zkoušky a přijatou referenční hodnotou (x_ref).

Výse uvedené definice jsou patrné z obrázku č. 1:

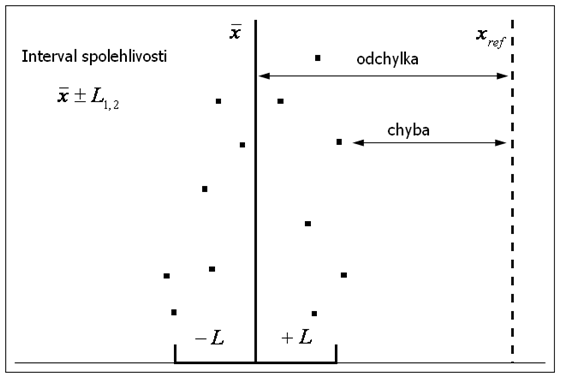
Interval spolehlivosti

Interval spolehlivosti (L_1,2) je interval, ve kterém s vysokou, předem zvolenou pravděpodobností leží hodnota hledaného parametru. Pokud bude provedeno další stanovení průměrné hodnoty za podmínek, při kterých byl stanoven interval spolehlivosti (L_1,2), pak s určitou pravděpodobností, obvykle 95%, „padne“ hodnota tohoto stanovení do intervalu spolehlivosti.

Grafické znázorění intervalu spolehlivoasti je znázorněno na obrázku č. 2:

Pro výpočet intervalu spolehlivosti se použije rovnice:

Nejistota měření

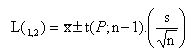
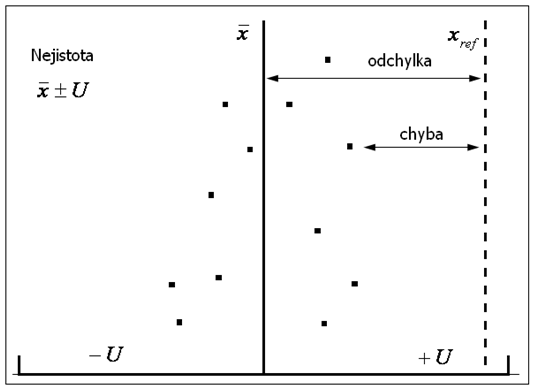
Nejistota měření (U) odpovídá intervalu, konstruovanému okolo výsledku měření tak, aby odrazil možnou variabilitu výsledků měření při uplatnění všech možných vlivů na měření a tedy poskytoval informaci o intervalu, o kterém lze určitou pravděpodobností, obvykle 95%, oprávněně předpokládat, že se v něm nachází skutečná hodnota měřené veličiny.

Nejistota měření je v současné době definována jako „parametr přidružený k výsledku měření, který charakterizuje míru rozptýlení hodnot, jež by mohly být důvodně přisuzovány měřené veličině“.

Grafické znázorění nejistoty měřehí je patrné z obrázku č. 3:

Standardní nejistota typu A (u_A) je způsobena náhodnými vlivy, jejíž příčiny nejsou známy. Hodnota nejistoty se zmenšuje se zvětšujícím se počtem opakování tzn. že se stanovuje z opakovaných měření za stejných podmínek. Platí pro přímo měřené veličiny.

Standardní nejistota typu B (u_B) vzniká ze známých a odhadnutelných příčin pocházejících z různých zdrojů. Nezávisí na počtu opakovaných měření.

Sloučení nejistot lze provést sumací kvadrátů nejistot typu A a B:

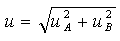
Standardní nejistota u(x_i). Nejistota výsledku měření vyjádřená ve formě směrodatné odchylky.

Kombinovaná standardní nejistota u_c(y). Standardní nejistota výsledku měření, je-li výsledek získán z hodnot odpovídajících několika dalším veličinám.

Rozšířená nejistota U. Veličina definující interval hodnot zahrnující výsledek měření, o němž lze předpokládat, že obsahuje velký podíl z rozdělení hodnot, které by mohly být důvodně přiřazeny k měřené veličině. U = k x u_c.

Koeficient rozšíření k. Číselný koeficient, jímž násobíme kombinovanou standardní nejistotu, abychom získali rozšířenou nejistotu.

Návaznost měření

Návaznost je vlastnost výsledku měření nebo hodnoty etalonu (standardu), kterou může být určen vztah k uvedeným referencím, zpravidla národním nebo mezinárodním etalonům (standardům), prostřednictvím nepřerušeného řetězce porovnávání, jejichž nejistoty jsou uvedeny.

Návaznost je v chemické analýze koncepcí poměrně novou a její uplatnění naráží na specifičnost chemické analýzy, zejména při analýze reálných matric. Zde každá přeměna vzorku (rozpouštění, hydrolýza, separace) znamená faktické přerušení řetězce porovnávání, jak vyplývá z definice návaznosti.

V hierarchii referencí návaznosti je nejvýše postavena jednotka SI, v chemické analýze látkové množství (mol). Na něj lze vztahovat prostřednictvím věrohodně definovaných čistých látek s věrohodným odhadem nejistoty obsahu dané látky. Ne vždy ale typ stanovované složky (např. vláknina, škrob, dusíkaté látky), charakter analyzovaného vzorku a vlastnosti použité metody takové zajištění návaznosti umožní. V takovém případě je další použitelnou referencí matriční referenční materiál, což je postup nejvhodnější.

Nejvhodnější způsob prokázání návaznosti je na základ E_n čísla (skóre), které je definováno pomocí nejistot měření:

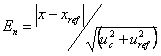
kde u_c je standardní nejistota získané hodnoty referenčního materiálu a u_ref je standardní nejistota referenční hodnoty referenčního materiálu x_ref.

Pro podmínku návaznosti pak můžeme psát:

0 < E_n < 2 návaznost prokázána

2 < E_n < 3 podezřelé výsledky

E_n > 3 návaznost nebyla prokázána.

[Top of Page]

Last modified: