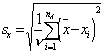
| Najít na této stránce: |
|
|
(1) |
|
|
(2a) |
|
|
(2b) |
Rmax = q.sx |
(3) |
|
n n= |
P, q |
||
|
0,90 |
0,95 |
0,99 |
|
|
2 |
2,33 |
2,77 |
3,64 |
|
3 |
2,90 |
3,31 |
4,12 |
|
4 |
3,24 |
3,63 |
4,40 |
|
5 |
3,48 |
3,86 |
4,60 |
|
|
(4) |
|
|
(5) |
yi = a + bxi |
(6) |
|
|
(7) |
|
|
(8) |
|
|
(9) |
y = box |
(10a) |
y = a + bx |
(10b) |
|
|
(11) |
|
|
(12) |
|
|
(13) |
|
|
(14) |
|
|
(15) |
|
|
(16) |
|
|
(17) |
|
|
(18) |
|
|
(19a) |
|
|
(19b) |
|
|
(20) |
|
|
(21) |
|
|
(22) |
|
|
(23) |
|
|
(23a) |
|
|
(23b) |
|
|
(24) |
|
|
(25) |
|
|
(25a) |
|
|
(25b) |
|
Pokus |
xA |
xB |
xC |
xD |
xE |
xF |
xG |
Účelová veličina yj |
|
1 2 3 4 5 6 7 8 |
+ + + - + - - - |
+ + - + - - + - |
+ - + - - + + - |
- + - - + + + - |
+ - - + + + - - |
- - + + + - + - |
- + + + - + - - |
y1 y2 y3 y4 y5 y6 y7 y8 |
|
Působení Wi |
WA |
WB |
WC |
WD |
WE |
WF |
WG |
|
|
xi(i=A- G) |
parametry analýzy, jejichž vliv na výsledek se zjišťuje |
|
yj(j=1-8) |
výsledek analýzy při daná kombinaci hodnot xA až xD |
|
+,- |
vyšší nebo nižší hodnota parametru xA až xG |
|
Wi(i=1-8) |
působení příslušného parametru xA až xG na výsledek y |
|
|
(26) |
|
|
(27) |
|
|
(28) |
|
|
(29) |
|
|
(30) |
|
|
(31) |
|
|
(32) |
|
|
(33) |
|
|
(34) |
|
|
(35) |
|
|
(36) |
|
|
nebo |
|
(37) |
|
|
(38) |
|
|
nebo |
|
(39) |
|
n |
a |
|||
|
0,10 |
0,05 |
0,02 |
0,01 |
|
|
3 |
0,886 |
0,941 |
0,972 |
0,988 |
|
4 |
0,679 |
0,765 |
0,846 |
0,889 |
|
5 |
0,557 |
0,642 |
0,729 |
0,760 |
|
6 |
0,482 |
0,560 |
0,644 |
0,698 |
|
7 |
0,434 |
0,507 |
0,586 |
0,637 |
|
8 |
0,399 |
0,468 |
0,543 |
0,590 |
|
9 |
0,370 |
0,437 |
0,510 |
0,555 |
|
10 |
0,349 |
0,412 |
0,483 |
0,527 |
|
|
(40) |
|
|
(41) |
|
|
(42) |